
Numerical Example of Linear Discriminant Analysis (LDA)
Here is an example of LDA. We are going to solve linear discriminant using MS excel.
You can download the worksheet companion of this numerical example here.
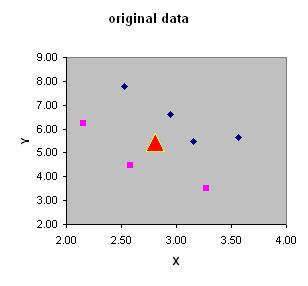
Factory "ABC" produces very expensive and high quality chip rings that their qualities are measured in term of curvature and diameter. Result of quality control by experts is given in the table below.
|
Curvature |
Diameter |
Quality Control Result |
|
2.95 |
6.63 |
Passed |
|
2.53 |
7.79 |
Passed |
|
3.57 |
5.65 |
Passed |
|
3.16 |
5.47 |
Passed |
|
2.58 |
4.46 |
Not Passed |
|
2.16 |
6.22 |
Not Passed |
|
3.27 |
3.52 |
Not Passed |
As a consultant to the factory, you get a task to set up the criteria for automatic quality control. Then, the manager of the factory also wants to test your criteria upon new type of chip rings that even the human experts are argued to each other. The new chip rings have curvature 2.81 and diameter 5.46.
Can you solve this problem by employing Discriminant Analysis?
Solutions
When we plot the features, we can see that the data is linearly separable. We can draw a line to separate the two groups. The problem is to find the line and to rotate the features in such a way to maximize the distance between groups and to minimize distance within group.
![]() = features (or independent variables) of all data. Each row (denoted by
= features (or independent variables) of all data. Each row (denoted by
![]() ) represents one object; each column stands for one feature.
) represents one object; each column stands for one feature.
![]() = group of the object (or dependent variable) of all data. Each row represents one object and it has only one column.
= group of the object (or dependent variable) of all data. Each row represents one object and it has only one column.
In our example,
 and
and
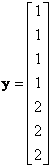
![]() = data of row
= data of row
![]() . For example,
. For example,
![]() ,
,
![]()
![]() = number of groups in
= number of groups in
![]() . In our example,
. In our example,
![]() = 2
= 2
![]() = features data for group
= features data for group
![]() . Each row represents one object; each column stands for one feature. We separate
. Each row represents one object; each column stands for one feature. We separate
![]() into several groups based on the number of category in
into several groups based on the number of category in
![]() .
.
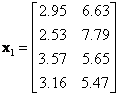 ,
,
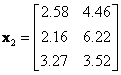
![]() = mean of features in group
= mean of features in group
![]() , which is average of
, which is average of
![]()
![]() ,
,
![]()
![]() = global mean vector, that is mean of the whole data set.
= global mean vector, that is mean of the whole data set.
In this example,
![]()
![]() = mean corrected data, that is the features data for group
= mean corrected data, that is the features data for group
![]() ,
,
![]() , minus the global mean vector
, minus the global mean vector
![]()
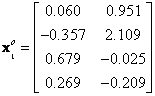 ,
,
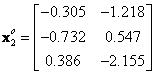
 = covariance matrix of group
= covariance matrix of group
![]()
![]() ,
,
![]()
![]() = pooled within group covariance matrix. It is calculated for each entry
= pooled within group covariance matrix. It is calculated for each entry
![]() in the matrix. In our example,
in the matrix. In our example,
![]() ,
,
![]() and
and
![]() , therefore
, therefore
![]()
![]() = prior probability vector (each row represent prior probability of group
= prior probability vector (each row represent prior probability of group
![]() ). If we do not know the prior probability, we just assume it is equal to total sample of each group divided by the total samples, that is
). If we do not know the prior probability, we just assume it is equal to total sample of each group divided by the total samples, that is
![]()
![]()
Discriminant function
![]()
We should assign object
![]() to group
to group
![]() that has maximum
that has maximum
![]()
The results of our computation are given in MS Excel as shown in the figure below.
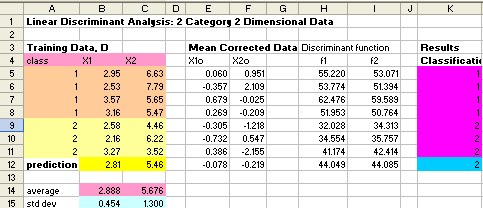
The discriminant function is our classification rules to assign the object into separate group. If we input the new chip rings that have curvature 2.81 and diameter 5.46, reveal that it does not pass the quality control.
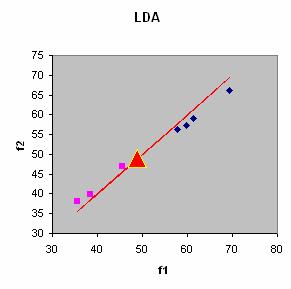
Transforming all data into discriminant function
![]() we can draw the training data and the prediction data into new coordinate. The discriminant line is all data of discriminant function
we can draw the training data and the prediction data into new coordinate. The discriminant line is all data of discriminant function
![]() and
and
![]() . In MS Excel, you can hold CTRL key wile dragging the second region to select both regions.
. In MS Excel, you can hold CTRL key wile dragging the second region to select both regions.
This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Discriminant Analysis Tutorial. http://people.revoledu.com/kardi/ tutorial/LDA/
